Parabola is a path traced by a point which moves in the plane in such a way that its distance from fixed point is always equal to distance from a fixed line.
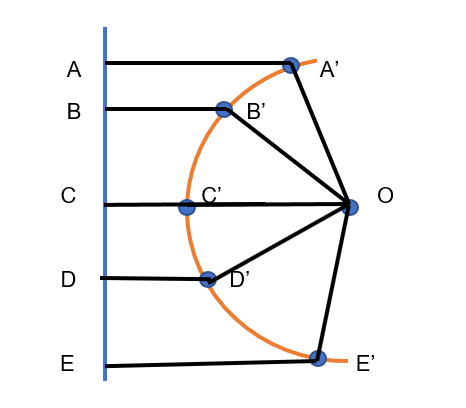
In the above figure O is the fixed point and the blue line is the fixed line. Now the path traced by point A’, B’, C’, D’ and E’ are such that;
- OA’ = AA’
- OB’ = BB’
- OC’ = CC’
- OD’ = DD’
- OE’ = EE’
Hence the path traced by point A’, B’, C’, D’ and E’ is said to be parabola.
The fixed point is said to be focus of parabola and the fixed line is said to be directrix.
Types of parabolas:
Right hand parabola (with vertex on origin)

Considering distance between focus and vertex to be “a” units (a>0), hence perpendicular distance between vertex and directrix will also be “a” units.
If we consider any point P (x, y) lying on the parabola, then as per definition of the parabola distance between this point P from the focus is equal to distance between point P and the directrix. Hence, we can say that
= √(x-a)2 +(y-0)2 = |x+0+a|/1 (Using distance formula)
Squaring both the sides;
(x-a)2 + y2 = (x+a)2
y2 = 4ax (Also known as general equation of right-hand parabola)
If the vertex of parabola is (h,k), then the equation of the parabola will become (y-k)2 = 4a(x-h)
Length of latus rectum = 4a units.
Left hand parabola (with vertex on origin)
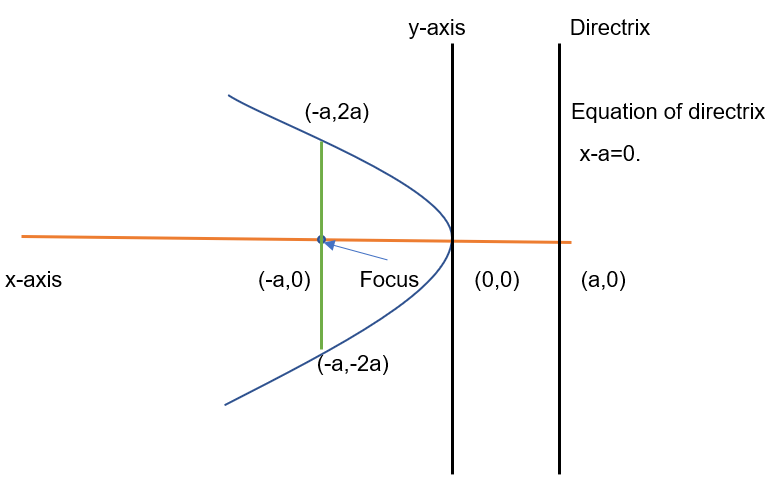
Considering distance between focus and vertex to be “a” units (a<0), hence perpendicular distance between vertex and directrix will also be “a” units.
If we consider any point P (x, y) lying on the parabola, then as per definition of the parabola distance between this point P from the focus is equal to distance between point P and the directrix. Hence, we can say that
y2 = -4ax (Also known as general equation of left-hand parabola)
If the vertex of parabola is (h,k), then the equation of the parabola will become (y-k)2 = -4a(x-h)
Length of latus rectum = 4a units.
Upward parabola (with vertex on origin)

Considering distance between focus and vertex to be “a” units (a>0), hence perpendicular distance between vertex and directrix will also be “a” units.
If we consider any point P (x, y) lying on the parabola, then as per definition of the parabola distance between this point P from the focus is equal to distance between point P and the directrix. Hence, we can say that
x2 = 4ay (Also known as general equation of upward parabola)
If the vertex of parabola is (h,k), then the equation of the parabola will become (x-h)2 = 4a(y-k)
Length of latus rectum = 4a units.
Downward parabola (with vertex on origin)
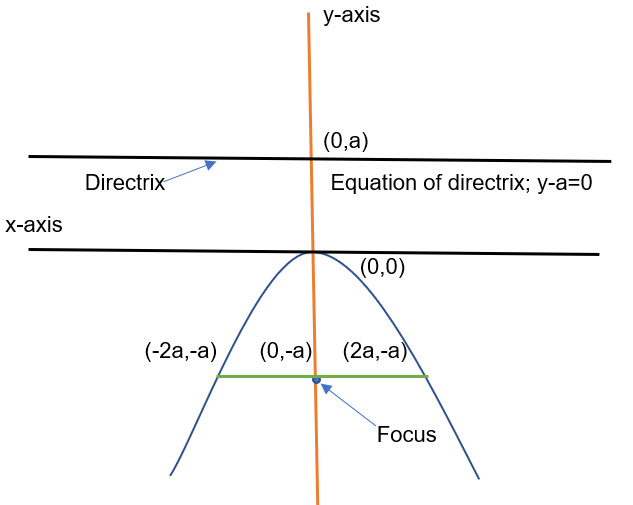
Considering distance between focus and vertex to be “a” units (a<0), hence perpendicular distance between vertex and directrix will also be “a” units.
If we consider any point P (x, y) lying on the parabola, then as per definition of the parabola distance between this point P from the focus is equal to distance between point P and the directrix. Hence, we can say that
x2 = -4ay (Also known as general equation of downward parabola)
If the vertex of parabola is (h,k), then the equation of the parabola will become (x-h)2 = -4a(y-k)
Length of latus rectum = 4a units.
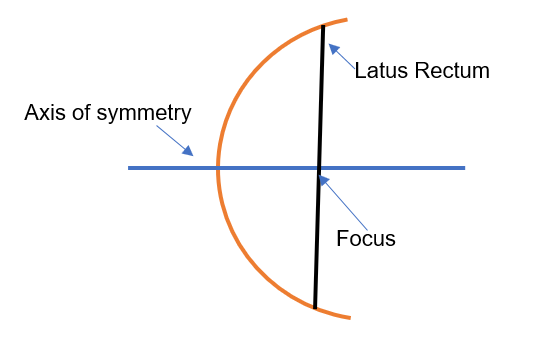
Important terminology related to parabola;
- Vertex
- Axis of symmetry
- Focal chord
- Focal distance of a point
- Latus Rectum
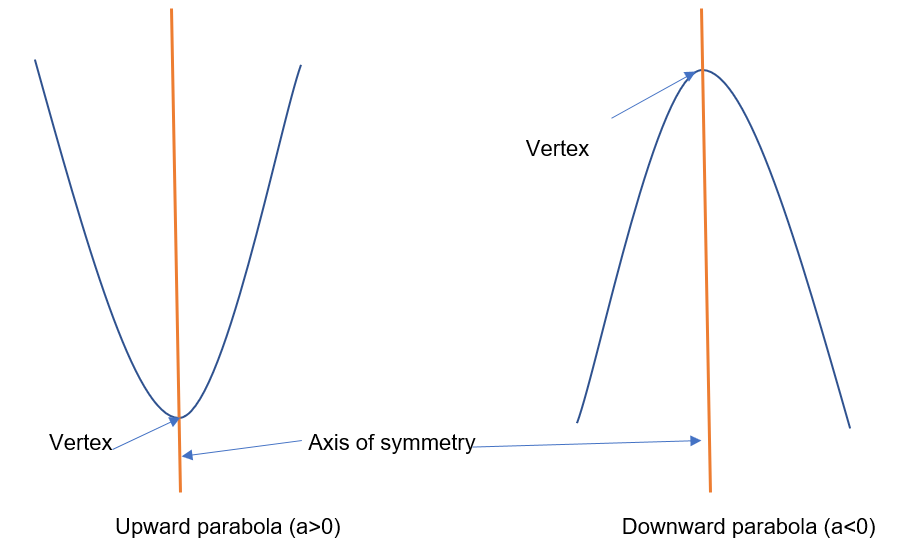
Vertex of a parabola is either highest point for downward parabola or lowest point for upward parabola.
Axis of symmetry is a line which passes through the vertex of the parabola and divides the parabola into two equal halves.
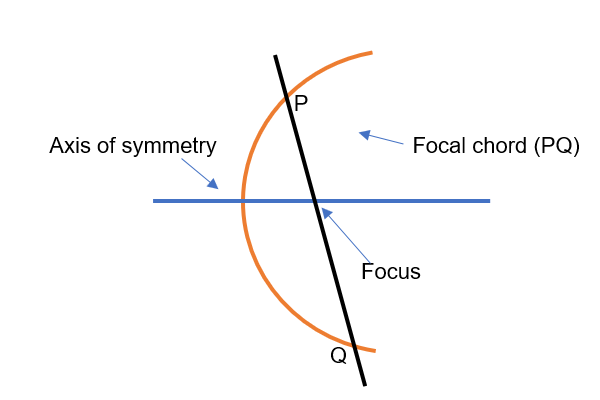
Focal chord is a line segment which passes through the focus of the parabola.
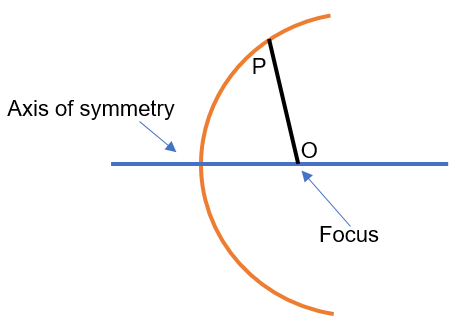
Focal distance of a point is nothing but distance between any point lying on the parabola and focus of parabola. In the below figure PO represents focal distance of point P.
Latus rectum of a parabola is line segment which passes through focus of the parabola and is perpendicular to the axis of parabola. End points of the latus rectum lies on the parabola.