Let me make it simple for each one of you!!

Let us understand both the concepts simultaneously in order to differentiate between the two by taking examples.

Lets say I have 10 different books in front of me and I wish to pick any 2 books randomly. Now the question comes does the order in which I’ll be picking the books would matter. And the answer is “No”.

Understand, what I asked was to pick books and not arrange them. Its like lets say suppose you need to select two players out of six players. Now the two players I wish to pick up are Shaun and Ron. Now think logically, the order wont matter because we are choosing two players. Right!! this choosing of things, where the order doesn’t matter is known as combination.

Formula for Combination is:

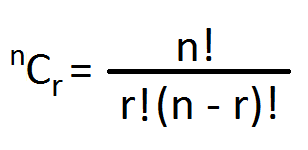
Now how to use this formula:- So let’s take the above example only where we need to choose two players out of six players. Hence the formula would become

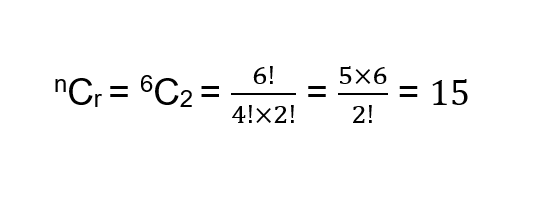
Now the question comes what is mean by the answer “15”. It means that there are 15 ways to choose any 2 players out of given 6 players.

Now, lets say there is an athletic meet in the school and a 100m race is about to happen and 7 participants will take part in the race. Now we know that the athlete who’ll finish first will get the gold medal, the one who’ll come second will get the silver medal and the one who’ll come third will get the bronze medal.

Hence, comes the ultimate question: “Whether the order in which athletes finish the race matters or not?”

And the answer is “yes”. Now someone may ask why the order matters now!! So, lets understand it this way

Lets say three athlete John, Ali and Athrav finish the race in the first three position. Now there can be multiple possibilities as far as the order in which they’ll finish the race. For example John can come first, Athrav can come second and Ali can come third or it may happen that Ali comes first, John comes second and Athrav comes third and so on and so forth, hence it is clear that here order matters.

Formula for Permutation is:

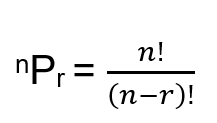
Now how to use this formula:- So let’s take the above example only where seven athletes take part in 100m race and we need participants for first three positions . Hence the formula would become

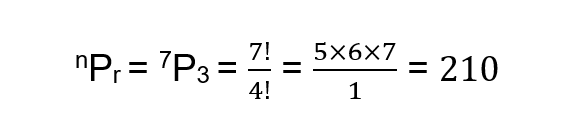
Now the question comes what is mean by the answer “210”. It means that there are 210 ways in which these seven athletes can finish the race.

So what did we learn? The difference between permutation and combination is all about whether the order matters or no!!

Now sometimes it happens that we aren’t able to figure out whether question is pertaining to combination (selection) or permutation (arrangement), so in that case we make use of counting method.

Remember two things in counting method, one is whenever we use the term “and”, it means multiplication and if we use the term “or”, it means addition.

Let’s take an example:

A questionnaire has four questions each of which has four options. Anyone filling questionnaire has to answer all the four questions. In how many ways can anyone answer all the four questions?

Let’s first understand the meaning of “In how many ways can anyone answer all the four questions”. So lets take example of three people filling up the questionnaire.

Let’s say person P fills the questionnaire as ABCD ( option A for first question, option B for second question, option C for third question and option D for fourth question ).

Person Q fill the questionnaire as BACD ( option B for first question, option A for second question, option C for third question and option D for fourth question ).

and, person R fills the questionnaire as DACB ( option D for first question, option A for second question, option C for third question and option B for fourth question ).

If you’ll observe carefully, you’ll realize that each one of them has marked ABCD to all the four questions; however the way in which they have marked it is different. P has marked option B for the second question, Q has marked option B for first question and R has marked option B for the fourth question.

So we need to figure out these total possible ways!!

Let’s look at questions individually, hence we can say that the first question can be answer is four possible ways, the second question can also be answered in four possible ways, same goes for the third and the fourth questions. Hence four possibilities for first question, four for second one, four for third one and fourth for the last one. Now, if anyone wants to fill in the questionnaire, he/she has to answer all the four questions, hence the first question and the second question, and the third question and the fourth question. Whenever we use “and” it stands for multiplication, hence 4 x 4 x 4 x 4 = 256 ways.

Hence there are 256 different ways of answering the questionnaire.

Let’s take example for “or”.

There are three cities, namely A, B and C. There are four ways of going from city A to city C and there are seven ways of going from city A to city B, where there is no common route to go city B or C. In how many ways can a person go from city A to city B or city C?

If a person wants to go from city A to city C, there are four ways, and if a person wants to go from city A to city B, there are seven ways. Now a person can either go to B or C, and whenever we use the term “or”, it stands for addition. Hence, 4 + 7 = 11ways.

To learn more, watch the below video

Space for YouTube Video

Try the below questions once you have gone through the above video;