Arithmetic Progression(AP)

In any series whenever any two consecutive terms have the same common difference, then that series is said to be in arithmetic progression. For example if series has terms such as 2,4,6,8,10…. In this series we can all see that common difference between any two consecutive terms is 2. Hence the series is in arithmetic progression with common difference of 2.

Points to remember;

First term of any AP is represented by “a”.

Common difference in AP is represented by “d”.

Hence, the terms of any AP can be written as a, a+d, a+2d, a+3d……….. up to a+(n-1)d. The term a+(n-1)d in AP is known as the general term of any arithmetic progression.

Hence we say, a_n = a+(n-1)d; where a_n represents the general term of AP. This formula is usually used to calculate things such as;

1. Any n^th term of arithmetic progression. For example if I want to calculate 37^th term of the AP. Hence using the formula, we can say that a₃₇ = a+(37-1)d = a+36d.
2. Last term of any AP, usually represented by the letter “l”. Hence, if we know the value of first term, common term and total terms; hence l = a+(n-1)d.

Apart from this, we also have formula to calculate the sum of first n terms of an Arithmetic Progression.

Geometric Progression(GP)

In any series whenever any two consecutive terms have the same common ratio, then that series is said to be in geometric progression. For example if series has terms such as 2,4,8,16,32…. In this series we can all see that common ratio between any two consecutive terms is 2. Hence the series is in geometric progression with common ratio of 2.

Points to remember;

First term of any GP is represented by “a”.

Common difference in GP is represented by “r”.

Hence, the terms of any GP can be written as a, ar, ar², ar³……….. up to ar^n-1. The term ar^n-1 in GP is known as the general term of any geometric progression.

Hence we say, a_n = ar^n-1; where a_n represents the general term of GP. This formula is usually used to calculate things such as;

1. Any n^th term of geometric progression. For example if I want to calculate 37^th term of the GP. Hence using the formula, we can say that a₃₇ = ar^37-1, hence a₃₇ = ar³⁶ .
2. Last term of any GP, usually represented by the letter “l”. Hence, if we know the value of first term, common term and total terms; hence l = ar^n-1.

Apart from this, we also have formula to calculate the sum of first n terms of an Geometric Progression.

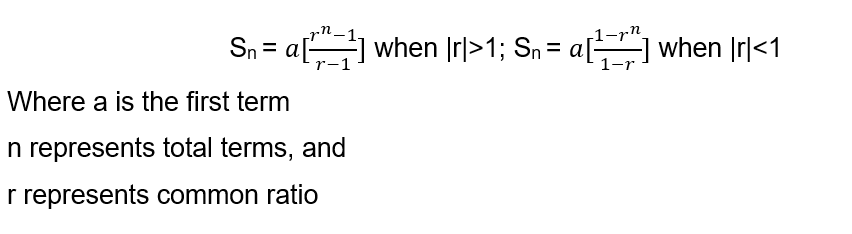
Space for YouTube Video

Try the questions given below, once you have gone through the above video;