
Any equation of the form y = ax2 + bx + c is known as quadratic equation or an equation of a parabola.
So coming to the discussion on how to calculate roots of the quadratic equation. If you are wondering what are roots of an equation or solutions of an equation read Functions-Basic
Now, there are two ways of calculating the roots;
- Splitting the middle term
- Using the formula
Let’s take examples for the above two cases.
Splitting the middle term:
Find out the roots of the quadratic function f(x) = x2+7x+12.
Since we need to find the roots of the equation, hence value of function should be equal to 0. Hence, x2+7x+12=0.
Now by using splitting the middle term, we can re-write the equation as x2+4x+3x+12=0.
Before we move on, let’s first understand the meaning of splitting of middle terms.
So, what we basically need to do is, we need to split the middle term (the x term with its coefficient) into two parts such that the product of two parts is equal to product of the first term and the constant term.
Like in the above case 7x can be re-written as (3x+4x) since 3x*4x =12x2 = x2 * 12.
Once done with the middle term splitting, we need to do the pairing.
(x2 + 4x) + (3x + 12) = 0
x(x+4) + 3(x+4) = 0;
(x+3)(x+4)=0
Which will finally give us the roots as – 3 and – 4.
Using the formula:
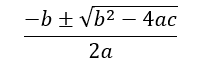
Where a is coefficient of x2
b is coefficient of x
and c is the constant term
So, considering the same equation x2+7x+12 , we can say that a = 1, b = 7 and c = 12.
And once we plug in the values in the above formula; we’ll realize that the roots are – 3 and – 4.
Now, you have understood both the ways of calculating roots, one doubt that will pop up in your mind will be which method shall I use?
So, I’ll give you a very straight forward answer; It depends on the question.
Okay now, let’s go through the conversation between Harshit and Athrav and try to understand if there are any way to make this easier.
Athrav: Hi Harshit, I need your help!!
Harshit: Okay, please ask?
Athrav: I am having hard time understanding which method to use to figure out the roots of the quadratic equation.
Harshit: Oh! You mean whether to choose splitting the middle term or to use the formula? Right?
Athrav: Yep. Right.
Harshit: Alright, let’s take few examples to understand.
x2 + 2x – 63
x2 + 3x + 7
4x2 + 4x + 1
x2 + 4x – 96
Let’s have a look at the first problem.
Now what you need to remember when you split the middle term is that first take the product of constant term and coefficient of x2, with their signs. So, in the first one the product will be – 63.
Now, what you need to do is to factorize – 63. So – 63 can be written as
-1 x 63;
-63 x 1;
-9 x 7;
-7 x 9
And so on and so forth. I think you can figure the rest by yourself.
Athrav: Yes Yes.
Harshit: Now, you need to figure out a pair whose sum is equal to 2x.
Athrav: Oh! That will be 9x and -7x.
Harshit: Yes, correct.
Hence you can split the middle term and re-write the equation as x2 + 9x – 7x – 63. Then the same process continues. I think you can do the rest.
Athrav: Yes. Can I have one more example?
Harshit: Sure! Let’s take example 2.
Now, when I’ll take the product of coefficient of x2 and constant term it will be 7. On factorizing it you’ll get
-7 x -1
7 x 1
And none of them when added will give us 3.
Hence splitting the middle term wont work here and we need to use the formula.
Athrav: Oh! Got it. But wait, so that means I’ll have to factorize the product every time and pen down all possibilities?
Harshit: No, not necessarily. Once you have practiced enough its going to be easy. Like for example, if I take example 3 which is 4x2 + 4x + 1
I’ll realize I can split the middle term as 2x and 2x and the product will be equal to product of 4x2 and 1.
Similarly, x2 + 4x – 96 can be written as x2 + 12x – 8x – 96.
Athrav: That was quick!! How do I get there?
Harshit: You’ll have to practice. There are no shortcuts. Try some 50 questions, you’ll get the hang of it.
To learn more, watch the below video

Space for YouTube Video
Try the below questions once you have gone through the above video;


