
First thing first, what is a straight line? A straight line or a line is nothing but collection of infinite points.
Before we actually start with understanding the concepts related to straight line, lets start with point.
So “point” in math is nothing but “an exact location”. A point has no dimension and is represented by a dot. When a point is extended in both the directions, it becomes a straight line.
Distance between two points.
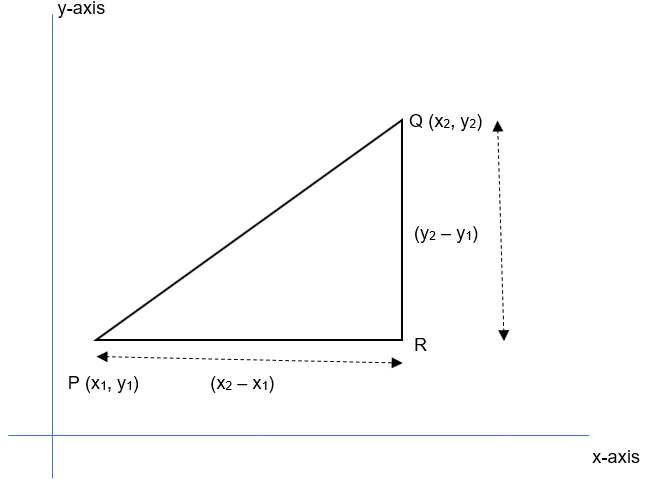
We need to calculate distance between points P(x1,y1) and Q(x2,y2). Remember one thing that x-coordinate of a point is nothing but perpendicular distance from y-axis and y-coordinate of a point is nothing but perpendicular distance from x-axis. Now since PR and QR are straight lines, hence we can say that coordinates or R would be (x2,y1). And hence length of PR would be x2 – x1 and length of QR would be y2 – y1.
Now, as we can see that triangle PQR is a right angle triangle hence we can use the Pythagoras theorem and say that PQ2 = PR2 + QR2.
Hence, PQ2 = (x2-x1)2 + (y2-y1)2 or we can say that PQ = √(x2-x1)2 + (y2-y1)2 , which is also known as the distance formula.
Remember one thing that the coordinates are to be taken with their respective signs. For example, if I ask you to calculate distance between points (-2,3) and (5,1), then according to formula,
PQ = √ (5 – (-2))2 + (1 – 3)2
= √ (7)2 + (-2)2
= √ 53
Slope of a line
Slope of a line is nothing but tanΘ, where “Θ” is the angle between line and x-axis made in anti-clockwise direction. Slope of a line is also known as inclination of a line.
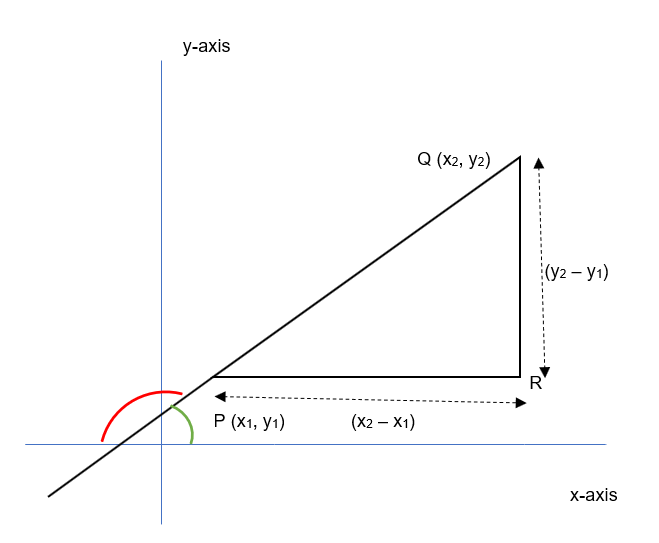
Angle made with green color has to be taken into consideration and not the angle made in red. Now since line PR is parallel to x-axis, hence we can say that angle QPR is also Θ. Now in a right angle triangle we know that tanΘ = opposite side / adjacent side or in short tanΘ = QR/PR; and hence
tanΘ = (y2-y1) / (x2-x1).
Points to remember:
- Two parallel line always have equal slope.
- Two perpendicular lines have product of their slopes = -1.
Internal and External division
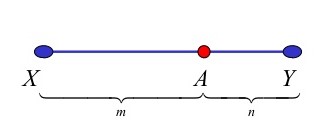
In the above case of internal division point A divides line XY in the ratio m:n. Lets assume coordinates of X to be (x1,y1) and Y to be (x2,y2), then coordinates of A will be
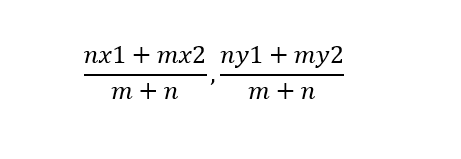
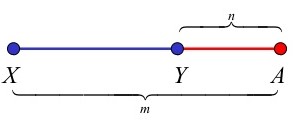
In the above case of external division point A divides line XY in the ratio m:n. Lets assume coordinates of X to be (x1,y1) and Y to be (x2,y2), then coordinates of A will be
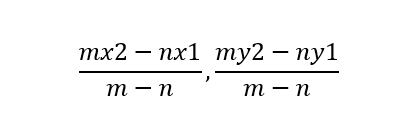
Equation of a line
General form: ax + by + c = 0
Slope-intercept form: y = mx + c where m is the slope and c is the y-intercept of the line.
y-intercept is nothing but y-coordinate of the point where line intersects y-axis. For example if a line intersects y-axis at (0,-7) then y-intercept is -7.
Apart from this you’ll also come across two point form, intercept form, etc. However all these forms are nothing but extrapolation of slope-intercept form.
Distance between point and a line & distance between two parallel lines
Lets consider a point P(x1,y1) and a line L having equation ax+by+c=0, then the distance between point P and line L can be calculated as
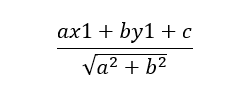
Please ensure that a, b, c, x1, y1 are taken with their respective signs.
If we have two parallel lines ax+by+c1=0 and ax+by+c2=0, then the distance between these two lines can be calculated as
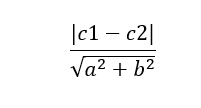

Space for YouTube Video
Try the questions given below, once you have gone through the above video.



